Integrales definidas
Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x = a y x = b. La integral definida es uno de los conceptos fundamentales del Análisis Matemático. La integral definida de f(x) en el intervalo [a,b] es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x = a y x = b (bajo la hipótesis de que la función f es positiva). Esta integral se representa por:
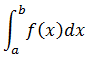
a es límite inferior de la integración y b es límite superior de la integración.
Si la función F es una función primitiva de f en el intervalo [a,b], por la Regla de Barrow se tiene que:
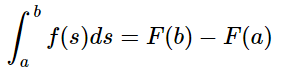
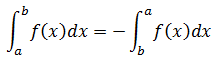
2. Si los límites que integración coinciden, la integral definida vale cero.
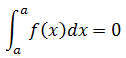
3. Si c es un punto interior del intervalo [a, b], la integral definida se descompone como una suma de dos integrales extendidas a los intervalos [a, c] y [c, b].
4. La integral definida de una suma de funciones es igual a la suma de integrales·
5. La integral del producto de una constante por una función es igual a la constante por la
integral de la función.
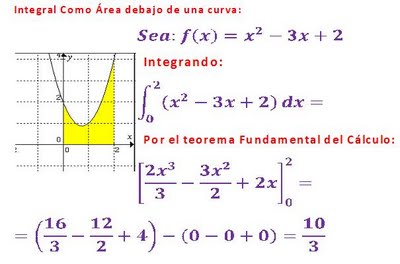
La imagen de ejemplo tiene un error en el primer término, al integrar x^2 queda x^3/3, luego al remplazar 2 en x, queda 8/3, siendo el resultado 2/3
Ejercicio 1.

Ejercicio 2.

Ejercicio 3.

Ejercicio 4.

Ejercicio 5.

Ejercicio 6.

Ejercicio 1 resuelto


Ejercicio 2 resuelto


Ejercicio 3 resuelto


Ejercicio 4 resuelto


Ejercicio 5 resuelto


Ejercicio 6 resuelto


No hay comentarios:
Publicar un comentario